Orbital Maneuvers

There are a number of objectives you might want to complete once you have reached orbit.  We will discuss entering a specified orbit, intercept trajectories, insertions into a formation of objects, and finally, earth-sun Lagrange points.  These sections build on one another to some degree.

Reaching a specific trajectory

When trying to reach a particular orbital trajectory, there are a number of factors you want to control. All orbital trajectories lie on a plane that passes through the center of the object you are orbiting.  Because of this, any two of these imaginary planes intersect along some line that passes through the center of the planet in question.  This is referred to as the line of nodes, pictured here (credit Orion 8 of wikimedia commons).  The Ascending and Descending nodes are located on either side of the line of nodes.  The differences between these nodes is arbitrary.  The nodes are the only two points where you can maneuver to align yourself with some intended trajectory.  This is because at these points your spacecraft is located inside the plane of the destination orbit.  You would then change your velocity in order to stay there.  You are typically thrusting in the normal or anti-normal direction, specified in this diagram (credit Adamhorvorka of wikimedia commons).  For reference, prograde is your direction of travel.

The remaining task when maneuvering to a specified trajectory is to match your apoapsis and periapsis with the target orbit.  These are the highest altitude and lowest altitude points in your orbit, respectively.  Assuming a start from a perfectly circular orbit, you would set your apoapsis by increasing your forward velocity, or thrusting in the prograde direction.  This increases your peak altitude because the earth is round, and in some cosmic sense any speed you add to yourself you keep.  As you accelerate forward, the planet starts to fall away from you, and that 'forward' velocity starts to carry you upward.  On the opposite side of the planet, you will have stopped ascending and reached your apoapsis.  This is because that burst of forward velocity has stopped pointing upward compared to the earth.  I have created a diagram to illustrate this, colored vectors are discussed with text of the same color.

At this point you may be thinking, 'wait a moment, doesn't this mean you will be travelling much slower at your apoapsis, since the added velocity is against the direction of motion?'  Yes, hypothetical you, that is exactly what happens.  Objects in an elliptical orbit like this are travelling much slower at their apoapsis.  As you reach your apoapsis, this added velocity will start to carry you back down again.  You prevent it from doing that by burning in the prograde direction and getting rid of it.  In some situations, you want to raise your periapsis (lowest point) and stop short of a circular orbit.  In that case you would only burn to get rid of part of that vector.

You will notice the red lines in my diagram form a line from the periapsis to the apoapsis.  The concept of this line is referred to by many names, here we will call it the argument of periapsis.  It is possible to have orbits that are identical from their argument of periapsis.  It would take a long time to explain how to adjust this parameter.  You will notice however, that your apoapsis is directly opposite from where you started your burn.  This will always be true.  You can use this to control where your periapsis and apoapsis will show up.  You wait until you are on the opposite side of a planet from your desired apoapsis, burn your engines until your math tells you you will reach the desired altitude, and then burn again to raise your periapsis to the desired altitude.

Intercept/Rendezvous Trajectory

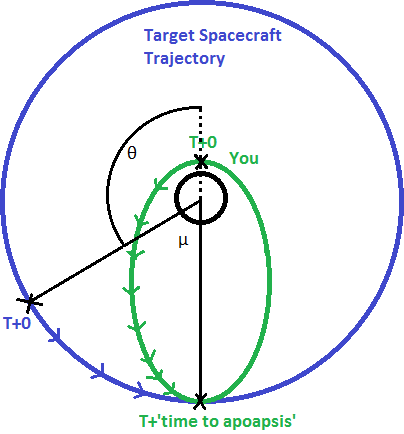
Now that we have covered the 'basics' I will discuss the idea of an intercept trajectory.  This is almost identical to the previous section, with the caveat that you need to reach a specific point at a specific time.  For reference I will assume you and your target are on circular trajectories, and you are below your target.  You will align planes at some point, but the key detail is when you decide to ascend to the targets altitude.  There is a certain amount of time it will take you to reach your apoapsis once you begin your ascent.  You want your target to be waiting for you when you get there, so that you can then match periapsis (and speeds, implicitly).  In order to do this, you have to calculate how far your target will travel during that time.  This can be expressed in degrees, referred to as μ in my diagram below.  You can use this to find your angle relative to the target, referred to as θ  (180 - μ).  This is called the phase angle.  Once you reach this relative position you can raise your apoapsis to the target and then match speeds.  This is in essence how you perform a rendezvous.

Insertion into a formation

In its simplest form, this is very similar to a Rendezvous.  You could imagine five sattelites forming a star, sharing the same trajectory.  In each case you would rendezvous with some imaginary satellite offset from some reference satellite a multiple of 72 degrees.  It can become considerably more complex in nature, but the basic concept remains the same.  In order to build a given constellation you need to enter a specific orbit at a specific place and time, in order to be positioned correctly relative to the other satellites.  This can vary hugely in nature, but in broad terms is put together using these concepts.  Pictured below is the GlobalStar communication satellite constellation, intended to provide continuous coverage to most of the surface of the earth.  Trajectories are in red and satellite positions in green. (source)

Earth-Sun Lagrange Points

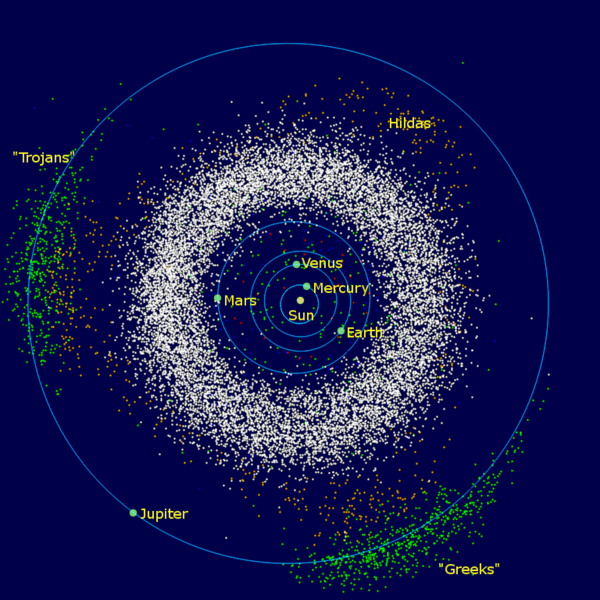
Lagrange points are conceptually interesting and useful locations, so I wanted to discuss them here.  There isn't any special trick to reaching them, you essentially boost straight towards them and then stop yourself.  Inspect this diagram in order to see the earth-sun lagrange points diagrammed (credit Xander89 of wikimedia commons).  As you can see, there are five of them.  What they essentially amount to is points of balance where the gravitational forces of the earth and sun allow objects to remain stable in not-quite-orbital trajectories.  L1 is probably the most intuitive, where the pull of the Sun and the Earth are in exact balance.  Essentially they allow you to remain stationary relative to the planet, at least in some reference frames.  The James-Webb space telescope will be position at L2 so that it can remain in the shade of the Earth.  This is part of their strategy to keep it cool so that its instruments can function properly.  L4 and L5 are stable, as is L3 to some degree.  The Jupiter-Sun L3-5 points contain various fields of asteroids trapped at these points, as can be seen below (credit Mdf at English Wikipedia).  Colored dots indicate objects trapped in the points.

To recap, we discussed how to insert yourself into a given trajectory.  Specifically, we discussed the concepts of aligning the plane of your orbit, and matching the positions of your apoapsis and periapsis.  We then discussed rendesvous, which amount to intercepting another vessel by reaching a point on their trajectory at the same time they do.  We then covered how you can use this idea to create formations of satellites.  Finally, we mentioned the earth-sun lagrange points.  In the next section we will talk about transferring to Moons orbiting the same thing you are orbiting, landing on them, and other such fun things.