Conclusion

Over the course of this blog series, we discussed the nature of human spaceflight as it exists today, which can be broken up into four major categories.  Ascent from a planets surface, maneuvers in orbit near a planet, transfer trajectories to the moon(s) of this planet, and interplanetary transfers which can vary significantly in complexity.  We will take this page to briefly recap everything that we covered here.  The ascent phase is one the most critical because, as mentioned, we cannot as yet produce spacecraft in space.

The ascent phase amounts to boosting into a fast enough trajectory that you never reach the ground.  In practical terms, this means leaving the atmosphere so that drag doesn't eventually slow you down and pull you down to the surface.  Therefore, one of the first steps is accelerating almost directly upwards to leave the thicker parts of the atmosphere.  The rocket then begins a turn which eventually leads to it burning sideways, in order to establish its trajectory.  It was noted that getting to orbit quickly is efficient, because you can spend less time fighting gravity.  Building up your sideways velocity is reserved for after you are most of the way out of the atmosphere so that you can build up lots of speed without burning up or being torn apart by atmospheric forces.  Once you have gotten away from the atmosphere, its a free run to orbit.

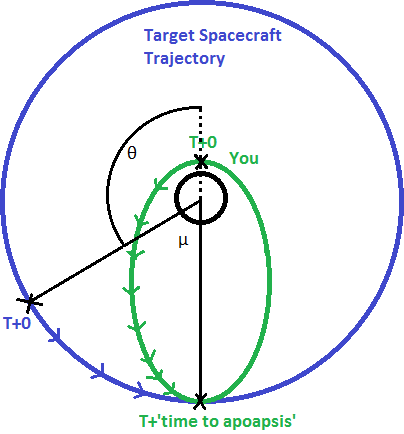
Orbit itself in this context refers to the space relatively close to Earth, or whichever arbitrary planet you have picked.  In general, whatever you want to do that doesn't involve orbiting some other object.  We discussed the principles behind how to perform a number of maneuvers.  This included raising and lowering your apoapsis and periapsis, rendezvous with another spacecraft or object, and inserting yourself into a formation.  We also explained the general concept of Earth-Sun Lagrange Points.  This wasn't a complete picture, but it covered a lot of the basics.

We then built on these concepts with the idea of transferring to a planet's moon.  We discussed how this in many ways amounts to a rendesvous with another spacecraft.  Very similar, except for the fact that as you approach the moon, its gravity begins to influence your trajectory.  We talked about the fuel savings associated with a 'suicide burn', which is somewhat similar to the reasoning behind flying very fast during the ascent phase.  It was also noted that inserting yourself into orbit around a moon is very similar to lowering your apoapsis during an orbital maneuver.

Next we discussed the basics of interplanetary transfers, and how they bear some resemblance to planet-moon transfers.  There was the idea of an escape trajectory, and how that in its barest form amounts to a co-orbit with the Earth.  Once in a co-orbit, you can essentially transfer to any planet in the system as if you were transferring to one of the Earth's moons.  In this case, one of the Sun's moons.  We noted how the point where you start your transfer burn could be seen as your launch window, and the ideal time to start your mission if you want to avoid months waiting around in space.  Finally, it was noted that settling into the orbit of another planet is very similar to settling into the orbit of a moon.

Finally, we discussed some of the more advanced techniques that could be used to achieve interplanetary transfers.  You can achieve orbit, or even a direct landing via aerobraking, where you intentionally descend into a planets atmosphere in order to slow yourself with the air drag.  Gravity assists were explained, although not as rigorously as previous concepts.  Lastly, we roughly characterized a continuous thrust trajectory, as well as why they exist.

All of these concepts combined give you a rough picture of what human spaceflight looks like today.  We launch our craft into orbit from the surface, and then perform various missions.  Perhaps we want to fly to the international space station, or build a constellation of sattelites.  Alternatively, we may want to fly to the Moon and insert ourselves into orbit, perhaps deploying landers.  Lastly, we may want to travel to another planet in our solar system.  There are many techniques we can use to make this cheaper.  This has been a long time hobby of mine, and I learned a lot while studying in order to write these blog posts.  I enjoyed making them, and hope you enjoyed reading them, at least to some degree.

Advanced Interplanetary Transfer

There are several techniques I would like to discuss that allow you to put together more sophisticated interplanetary transfers.  Not all of them can be reasonably described in terms of the previous post (basic interplanetary transfers).  Nevertheless I would like to characterize them as well to some degree.  First I will discuss aerobraking, then gravity assists, and finally continuous thrust trajectories that came with the advent of ion drives.

Aerobraking is the general process of reducing your velocity relative to a planet for free.  Free here meaning you don't have to spend fuel in the process.  The big downside is you need protection from the atmosphere of some kind unless you are performing a relatively gentle maneuver.  The concept of aerobraking is diving into a planets atmosphere, and using the drag in order to slow yourself down.  The atmosphere of a planet is effectively stationary relative to a planet, so it will keep trying to slow you down until you have effectively stopped relative to the planet.  In actuality, it is stationary relative to the surface of the planet, so it will effectively have some velocity.  This can be used to lower the apoapsis of your orbit, via principles discussed previously, or it can be for the purpose of leaving orbit entirely and landing on the surface.  In general the amount of velocity you bleed off is related to how close you come to the surface of a planet in the process.  Aerodynamics is extremely complex, so the amount of speed it is possible to bleed off can vary significantly.  Different spacecraft will get different results.

I don't have quite as satisfactory an explanation for gravity assists.  I will try to lean on your spatial intuition to give you some kind of idea.  Imagine you are riding a bike into a valley, as pictured below: 

You could expect yourself to come out the other side of the valley at more or less the same speed.  Now imagine that the valley is moving forward at a substantial speed as you come into it.  Gravity is strong enough to keep pulling you to the bottom of the valley, but you can feel the valley pulling you forward.  By the time you reach the other side you have gained a bunch of speed from the movement of the valley.  This is basically how a gravity assist works.  You may have seen a diagram like this before (credit AllenMcC from wikipedia):

These are actually a pretty good metaphor for the effects of gravity.  A cross section of that would resemble a valley.  Travelling through that gravitational valley while Jupiter is moving around the sun allows you to pick up quite a bit of speed.  Jupiter has been a common target of gravity assists, and by the law of conservation of energy is actually slightly slowed by every spacecraft that has utilized it.  The amount of energy that Jupiter loses (and the amount that you gain) is equal to the gravitational effects of your spacecraft on the entire mass of Jupiter.  A reverse gravity assist if you will.  Jupiter is immense, so this amounts to quite a bit of energy that you are gaining.

The general utility of this sort of maneuver is that you can get some free forward velocity to throw you onto a higher orbit on your way to your destination.  As to how exactly you would go about making use of that, that is a much more complicated question.  It doesn't really map to the more simplistic stuff we discussed earlier.  I'll close this section out with a diagram of the probe Rosettas trajectory, which made use of multiple consecutive gravity assists over the course of its ten year flight.  (courtesy of the ESA)

The last thing that I wanted to discuss was a continuous thrust trajectory.  Out of all of them it is probably the most alien to what we have discussed previously, in some ways.  The trajectories overall resemble a basic interplanetary transfer, due to the excess of fuel that tends to be available (relatively few gravity assists and such).  Ion drives have until recently been something of a fictional technology.  Very high specific impulse, but very low thrust.  Due to the low thrust, you have to fire your engines continuously for a long time in order to reach escape velocity and eventually ascend (or descend) to your destination.  The reason this low thrust is considered tolerable is because of the specific impulse factor that I have mentioned.  Imagine you are sitting on a skateboard and have three basketballs at your disposal.  You want to get moving, and in this example can only propel yourself by throwing the basketballs.  Will you choose to throw them really hard, or will you gently toss them in order to get yourself moving?  The answer will probably be throw very hard.  This is the general idea behind high specific impulse.  Ion drives throw the fuel very very hard (at very high speed, at least compared to rockets), so you need less fuel in order to change your speed by a certain amount.  The only downside is they can't throw lots of fuel at once, so there is relatively minimal thrust.  You might be throwing basketballs really fast, but the multi-ton probe is hardly budging.  The physical reason this works is because of the idea of impulse and momentum.  When you throw something, you impart a certain momentum.  The mass of the object multiplied by its speed.  That momentum gets transferred back to you in the opposite direction per Newtons Third Law.  The higher the speed, the more momentum you gain.  This allows spacecraft to get a lot more momentum out of their fuel and do a lot more maneuvering over the course of their missions.  The downside of the low thrust is that it greatly complicates entering and leaving gravity wells.  Dwarf planets and asteroids are generally easier to deal with as far as that goes.

I implied that Ion drives entered use at some point.  The recent Dawn mission utilized Ion drives, and was able to pack enough fuel to visit two dwarf planets over the course of its mission, entering into orbit of both (rather than a measly flyby).  Ceres and Vesta, if you were wondering.  You can look up lovely high resolution maps of both planets because of that mission.  Here is a diagram of its continuous thrust trajectory, courtesy of NASA:

As you can see, the thrust wasn't entirely continuous, but it most definitely was not freefall.

To recap, we discussed the concept of aerobraking.  Diving into an atmosphere to reduce your velocity relative to a planet, specifically relative to its surface.  The idea of a gravity assist, as well as a metaphor to describe how it allows you to gain speed.  Finally, continuous thrust trajectories were described, as well as the reason that they exist.

Basic Interplanetary Transfer

The basis of traveling between two planets can be broken into three main concepts.  Escape from the gravity well of your starting point, adjusting your trajectory to intercept your destination, and capturing yourself in your destinations gravity well.  This will be building on concepts from previous blog posts.

We will first discuss the idea of inserting yourself into an escape trajectory.  We will assume that you are starting in orbit of the earth.  An escape trajectory essentially amounts to raising the apoapsis (peak altitude) of your orbit to some altitude where the Earth's gravity is negligible.  In other words, putting yourself onto a trajectory where you have escaped the Earth's gravitational influence.  Once you start to approach your apoapsis on this escape trajectory, the Earth will definitionally stop influencing your velocity (and therefore trajectory).  Imagine that you have given yourself just enough velocity to reach this point.  You have come to a standstill just as Earth's gravity has lost its grip on you.  This leaves you in a co-orbit around the Sun on almost exactly the same trajectory as the Earth.  Indeed, for all intents and purposes you are orbiting the Sun and are preparing to travel to one of its moons.

This leads to the second part of the post, creating an intercept trajectory.  Lets assume you want to travel to Mars, since it is in a higher orbit around the Sun than the Earth is, allowing for a direct analogy to the previous post.  Just like when you were flying to the Moon in the previous post, there is a certain point in your orbit where you want to accelerate in the prograde direction so that you can intercept your destination.  This point is what is generally referred to as a launch window.  For a direct flight to Mars (we will discuss less direct methods of travel in the next post) the ideal time to launch your spacecraft is when the Earth is in that position.  This is because, as described earlier, you are on a trajectory that leaves you stationary relative to the Earth.  If you are effectively at the Earth, then you may as well leave your spacecraft on the Earth until you are ready to immediately start flying to Mars, rather than sitting for months or years in your co-orbit waiting to start your flight.  There is less time for things to break, and in the case of manned missions, you don't need to bring as much food and various assorted life support.

In this situation you would launch once the Earth is in position to allow an intercept with Mars, escape the Earth, and then perform the intercept burn in order to travel to Mars.  This is not, however, exactly how it is done.  Frequently there is what is called an 'ejection burn', where you accelerate onto an escape trajectory, and then keep accelerating until you have achieved an intercept trajectory with your destination.  This is essentially combining the two steps into one long acceleration burn.  This is for various reasons more efficient.  I wont explain every reason, but I will try to explain one of them.

A strange artifact of physics is that it is more efficient to fire your engines deep within a gravity well.  That is to say, it generates more mechanical energy than otherwise.  This is called the Oberth Effect.  The basis of the theory is the equation dictating how much energy you gain when accelerating.  The energy you can is equal to force times distance (W = F*d).  Your engines generate the same force no matter what, and over a certain period of time use the same amount of fuel no matter what.   So more distance over the same period of time means you get more energy for the same fuel.  How do you do that?  Well, you need more velocity.  You could imagine your spacecraft in its co-orbit, stationary relative to the Earth, vs it having all of the Earth's velocity plus whatever velocity it needs to stay in orbit around the planet.  This can lead to much higher speeds.  Therefore, it is more efficient to perform your intercept burn while close to the Earth, since gravity is leeching away your precious velocity as you climb out of the gravity well.  Using this concept, it is sometimes possible to gain more energy than the chemical energy stored in the rocket fuel.  This somewhat surreal fact allows for more efficient travel between planets.

Once you have achieved your basic interplanetary transfer trajectory, the final phase is to capture yourself in the orbit of the destination planet.  This essentially amounts to an escape velocity burn in reverse.  You will arrive at Mars at well over the escape velocity for the planet, and will carry on past it unless you do something.  This generally amounts to a retrograde burn in order to bring your apoapsis down to within the gravity well of Mars, much like a transfer to the Moon from low orbit.  Typically you can achieve this with your engines, although this is not the only option.  At this point you have successfully reached Mars, and can perform whatever mission you went there to carry out (building a space-cabin on Mars, perhaps).

To recap, we discussed the concept of an escape trajectory, and how this allows us to re-use the idea of planet to moon transfers for planet to planet transfers.  We then discussed the Oberth effect, and how this encourages us to complete our intercept burn while still close to the Earth, rather than taking things slowly by first escaping from the Earth and then setting up our intercept trajectory.  Finally, we talked about achieving orbit around Mars.

Planet-Moon Maneuvers

Generally speaking, a transfer to the Moon will be very similar to a rendezvous maneuver as discussed earlier, except with the added detail that you have to contend with the Moon's gravity.  As a result, this post will be building on the previous postings.  What we will discuss here applies to planets that have moons in general, but I will mostly discuss Earth and Luna for the purposes of this post.  I will also discuss landing on the Moon to some degree.

In most cases you want to transfer into some kind of orbit around the Moon, from some lower orbit around the Earth.  Most moons are on a 'prograde' orbit relative to the planet, they orbit in the same direction as the planets rotation.  This means that when you perform an efficient launch as discussed in the first post, you will be orbiting in the same direction as any moons.  The significance of this is the fact that you will very rarely have to intercept a moon head-on, and will instead be going in the same direction as them.  This reduces the fuel cost of matching speeds with them considerably.  Luna is no exception, though interestingly Triton is on a retrograde (opposite of prograde) orbit around Neptune.

Rendezvous with a moon is complicated by a couple of factors.  First, a perfectly executed rendezvous would lead to a collision with its surface.  Therefore, you need to deliberately miss at least slightly.  Second, its gravity will actively mess with your trajectory, especially if it is a big moon like Luna is.  This second factor is actually the key to missing the Moon.  Lets look at the intercept trajectory diagram from last post.

As far as we can see here, we are pretty much going to smack into the moon as planned.  Lets modify the diagram to show how the Moon's gravity is effecting our space craft.  The orange vectors indicate this.

You will notice there is a certain net 'leftward' acceleration the moon is imparting on our spacecraft.  This will in fact cause it to swing past the Moon when it would have otherwise collided with it.  In rough terms, exerting thrust to lengthen or shorten the 'leftward' part your velocity vector will allow you to control your periapsis (minimum altitude) above the Moon.  Or in other words, you control the extent to which you miss the Moon.  Once you are at your periapsis, you have to decelerate relative to the Moon in order to establish your orbit.  This is identical in nature to orbital adjustment maneuvers discussed in the previous post.  In general you would want to reduce your speed until you have a circular orbit.

After this point, you may want to attempt a landing.  The first step is to decelerate until your trajectory intersects the surface of the Moon.  The exact details of this trajectory are relatively unimportant, save the fact that you are de-orbiting yourself somehow and falling into the planet on a ballistic trajectory (you were doing so previously, but now something is in your way).  Efficient powered landings bear a certain similarity to the efficient takeoffs discussed in the second post.  You in general want to use your engine as little as possible to save fuel, which means slowing down relative to the surface at the absolute last second.  This is because you are fighting the Moon's gravity.  You could imagine a series of increasingly cautious landings, where you are continuously decelerating to keep your velocity at a comfortable level rather than allowing gravity to continuously speed you up.  Eventually you are being so cautious that you are hovering in place, and your landing will take infinite fuel and infinite time.  The opposite extreme of this is what is fondly referred to as the 'suicide burn' and is the most efficient landing technique out there.  You wait until the absolute last second, then fire your engines at full power to kill all of your velocity just before you reach the surface.  Generally missions are a little more cautious than this, because if you start the burn late then you will slam into the surface, generally at traumatically high speeds.  Usually powered landings will resemble this in some form or fashion, with very little deceleration until you are close to the surface.

This concept raises the possibility of a relatively interesting landing procedure.  When arranging to miss the Moon, instead adjust that leftward velocity vector to zero, deliberately setting a collision course with the Moon.  You could at this point conceivably land directly on the Moon via a suicide burn.  This general idea has been discussed in the past, and is referred to as a Direct Descent.  Unexpected engine failure, or unusually slow engine startup time would most likely be a death sentence for your vessel, so it is generally not seriously considered.  I find it to be a fun concept to imagine however, worth trying in Kerbal Space Program if nothing else.

To recap, we discussed transferring from the orbit of a planet to one of its moons.  In practice, we used Earth and Luna to discuss this idea.  We mentioned the fact that the Moon, as is typical, is on a prograde orbit around the Earth.  This makes it cheaper to travel there since its easier to launch spacecraft in a prograde orbit, and it would be harder to transfer to the Moon from a head on approach.  We talked about how the Moon's gravity will modify your approach trajectory and generally cause you to miss.  We then discussed how you can manipulate this in order to control your altitude once you reach the Moon.  Finally, we discussed landing procedures.

Orbital Maneuvers

There are a number of objectives you might want to complete once you have reached orbit.  We will discuss entering a specified orbit, intercept trajectories, insertions into a formation of objects, and finally, earth-sun Lagrange points.  These sections build on one another to some degree.

Reaching a specific trajectory

When trying to reach a particular orbital trajectory, there are a number of factors you want to control. All orbital trajectories lie on a plane that passes through the center of the object you are orbiting.  Because of this, any two of these imaginary planes intersect along some line that passes through the center of the planet in question.  This is referred to as the line of nodes, pictured here (credit Orion 8 of wikimedia commons).  The Ascending and Descending nodes are located on either side of the line of nodes.  The differences between these nodes is arbitrary.  The nodes are the only two points where you can maneuver to align yourself with some intended trajectory.  This is because at these points your spacecraft is located inside the plane of the destination orbit.  You would then change your velocity in order to stay there.  You are typically thrusting in the normal or anti-normal direction, specified in this diagram (credit Adamhorvorka of wikimedia commons).  For reference, prograde is your direction of travel.

The remaining task when maneuvering to a specified trajectory is to match your apoapsis and periapsis with the target orbit.  These are the highest altitude and lowest altitude points in your orbit, respectively.  Assuming a start from a perfectly circular orbit, you would set your apoapsis by increasing your forward velocity, or thrusting in the prograde direction.  This increases your peak altitude because the earth is round, and in some cosmic sense any speed you add to yourself you keep.  As you accelerate forward, the planet starts to fall away from you, and that 'forward' velocity starts to carry you upward.  On the opposite side of the planet, you will have stopped ascending and reached your apoapsis.  This is because that burst of forward velocity has stopped pointing upward compared to the earth.  I have created a diagram to illustrate this, colored vectors are discussed with text of the same color.

At this point you may be thinking, 'wait a moment, doesn't this mean you will be travelling much slower at your apoapsis, since the added velocity is against the direction of motion?'  Yes, hypothetical you, that is exactly what happens.  Objects in an elliptical orbit like this are travelling much slower at their apoapsis.  As you reach your apoapsis, this added velocity will start to carry you back down again.  You prevent it from doing that by burning in the prograde direction and getting rid of it.  In some situations, you want to raise your periapsis (lowest point) and stop short of a circular orbit.  In that case you would only burn to get rid of part of that vector.

You will notice the red lines in my diagram form a line from the periapsis to the apoapsis.  The concept of this line is referred to by many names, here we will call it the argument of periapsis.  It is possible to have orbits that are identical from their argument of periapsis.  It would take a long time to explain how to adjust this parameter.  You will notice however, that your apoapsis is directly opposite from where you started your burn.  This will always be true.  You can use this to control where your periapsis and apoapsis will show up.  You wait until you are on the opposite side of a planet from your desired apoapsis, burn your engines until your math tells you you will reach the desired altitude, and then burn again to raise your periapsis to the desired altitude.

Intercept/Rendezvous Trajectory

Now that we have covered the 'basics' I will discuss the idea of an intercept trajectory.  This is almost identical to the previous section, with the caveat that you need to reach a specific point at a specific time.  For reference I will assume you and your target are on circular trajectories, and you are below your target.  You will align planes at some point, but the key detail is when you decide to ascend to the targets altitude.  There is a certain amount of time it will take you to reach your apoapsis once you begin your ascent.  You want your target to be waiting for you when you get there, so that you can then match periapsis (and speeds, implicitly).  In order to do this, you have to calculate how far your target will travel during that time.  This can be expressed in degrees, referred to as μ in my diagram below.  You can use this to find your angle relative to the target, referred to as θ  (180 - μ).  This is called the phase angle.  Once you reach this relative position you can raise your apoapsis to the target and then match speeds.  This is in essence how you perform a rendezvous.

Insertion into a formation

In its simplest form, this is very similar to a Rendezvous.  You could imagine five sattelites forming a star, sharing the same trajectory.  In each case you would rendezvous with some imaginary satellite offset from some reference satellite a multiple of 72 degrees.  It can become considerably more complex in nature, but the basic concept remains the same.  In order to build a given constellation you need to enter a specific orbit at a specific place and time, in order to be positioned correctly relative to the other satellites.  This can vary hugely in nature, but in broad terms is put together using these concepts.  Pictured below is the GlobalStar communication satellite constellation, intended to provide continuous coverage to most of the surface of the earth.  Trajectories are in red and satellite positions in green. (source)

Earth-Sun Lagrange Points

Lagrange points are conceptually interesting and useful locations, so I wanted to discuss them here.  There isn't any special trick to reaching them, you essentially boost straight towards them and then stop yourself.  Inspect this diagram in order to see the earth-sun lagrange points diagrammed (credit Xander89 of wikimedia commons).  As you can see, there are five of them.  What they essentially amount to is points of balance where the gravitational forces of the earth and sun allow objects to remain stable in not-quite-orbital trajectories.  L1 is probably the most intuitive, where the pull of the Sun and the Earth are in exact balance.  Essentially they allow you to remain stationary relative to the planet, at least in some reference frames.  The James-Webb space telescope will be position at L2 so that it can remain in the shade of the Earth.  This is part of their strategy to keep it cool so that its instruments can function properly.  L4 and L5 are stable, as is L3 to some degree.  The Jupiter-Sun L3-5 points contain various fields of asteroids trapped at these points, as can be seen below (credit Mdf at English Wikipedia).  Colored dots indicate objects trapped in the points.

To recap, we discussed how to insert yourself into a given trajectory.  Specifically, we discussed the concepts of aligning the plane of your orbit, and matching the positions of your apoapsis and periapsis.  We then discussed rendesvous, which amount to intercepting another vessel by reaching a point on their trajectory at the same time they do.  We then covered how you can use this idea to create formations of satellites.  Finally, we mentioned the earth-sun lagrange points.  In the next section we will talk about transferring to Moons orbiting the same thing you are orbiting, landing on them, and other such fun things.

Ascent

The future is coming.


In my first post I mentioned that re-usability would immensely cheapen space travel, specifically the ascent to orbit phase of space travel.  This is because fuel costs are vanishingly tiny compared to the cost of the rockets themselves, around $200k vs. $60,000k.  Therefore, ability to recover and re-use the rocket is key.  Pictured above is a recent long exposure of a SpaceX Falcon 9 launch, and the successful recovery of its first stage.  This was the first time the company succeeded in doing so.  The system is imperfect, there are repair and refit costs (the rocket is generally damaged by temperature changes during descent), and they have no way to recover the second stage.  However, they estimate that they will be able to save around 30% with things as they are.  They hope to continually ruggedize the design and eventually reduce launch costs to somewhere within the region of one million dollars per launch.

The United Launch Alliance, old guard of the payload carrying rocket industry, have been working on the Vulcan, their own re-usable design.  The details of this system remain vague, for now.

The profile of a typical rocket launch consists of a couple of phases.  In the first phase, you are boosting upward to begin ascending to get out of the thick parts of the atmosphere.  In the second phase, you begin rotating and thrusting to the side in order to achieve orbit.  This is the part where you are thrusting sideways until the earth curves away under your trajectory and you lose the ability to reach the ground.  Generally the people designing the launch profile are trying to balance destroying the rocket with aerodynamic forces and getting into orbit as quickly as possible.  There tends to be a (more or less) straight upward portion of the launch where you focus on leaving the atmosphere quickly, so that you can build up your sideways velocity without destroying yourself.  They want all of this to happen quickly in order to save fuel.  I explained earlier that fuel is cheap, however adding more fuel will exponentially increase the total size of the rocket.  Rockets are expensive, so you want to use as little fuel as possible in order to have a smaller rocket.

Anyways, rapidly ascending saves you fuel because you are fighting gravity.  Imagine a series of rocket launches with lower and lower rates of upward acceleration.  Eventually you are left with a rocket that is hovering in place, which would require infinite fuel in order to make orbit.  As you increase your acceleration (decrease the ascent time), you asymptotically approach a fuel cost equal to the difference in energy between sitting on the launch pad and coasting along in orbit at high speed.  They haven't reached that ideal, but that is in part why rockets tend to break the sound barrier as a matter of course.  It would be wasteful not to do it that way.

Generally speaking, cargo rockets like the Falcon 9 ditch their first stage well after they have begun thrusting down range.  Its therefore somewhat fuel-intensive to turn completely around and return to the launch pad.  In fact, when lifting especially heavy payloads it is impossible.  SpaceX's solution to this was to try to land the rocket on a drone ship out on the ocean, downrange from the launch site.  After several failures, they recently succeeded in doing so, as part of a supply run to the ISS.

Direct Link

To quickly recap, a critical cost saving measure for space travel is re-using the rocket.  The fuel is much cheaper than the rocket itself, so if you can re-use the rocket then things are great.  SpaceX and the United Launch Alliance have both been working on ways to achieve this.  You also want to be able to ascend quickly, in order to save fuel and keep rockets down to a manageable size.  Finally, rockets generally want to ascend directly upwards before curving their trajectory so that they don't destroy themselves on the atmosphere.  In my next post I will talk about some of the basic things you can do once you have reached orbit.

Introduction

This blog will be discussing the fundamentals of orbital maneuvers.  This is a hobby of mine that I enjoy studying from time to time.

Maneuvering in space can be made into a very fine art, if you are interested in efficiency.  Efficiency, in point of fact, tends to be a paramount concern.  While you can in fact simply point your vessel towards your destination and fire your engines until you get there, this is extremely wasteful in terms of fuel (though it is very fast).  Though there are efficient methods of travel that involve continuous burns, this involves very high specific impulse and low thrust engines.  The high thrust variant wont be remarked upon here in any great length.  Fear not however, specific impulse and thrust will be explained, most likely in the first section.

In this blog I will cover five main topics pertaining to this.

Ascent:
Given the planet-bound nature of our civilization in this day and age, lifting our various fancy machinery from the planet into orbit is a key element of space travel in all regards.  Nobody is able to do serious fabrication in orbit of yet, however that may one day become a reality.  For now, however, we need to make things down here.

The silver bullet for efficient ascent right now is a fully re-usable cargo rocket.  Most payloads are delivered to orbit atop rockets that cost sixty million (USD) or more to produce.  These devices are generally allowed to crash unceremoniously into the ocean at high velocities.  Currently SpaceX pegs the fuel cost at approximately $200,000 per launch.  As you can probably infer, being able to recover the launch system fully intact and operational would cheapen space flight quite a bit.

Orbital Maneuvers and Key Locations:
Once you have escaped the atmosphere, you generally want to go somewhere specific.  There are many such places.  You might want to rendezvous with a space station, position yourself in some kind of constellation relative to other sattelites, or position for some kind of transfer to another celestial body.  Finally, you might want to travel to a Lagrange Point.  If you picked L4 or L5, then you can be reasonably certain your devices debris will be admired millions of years from now (how rude).

Planet-Moon transfers and Maneuvers:
This is somewhat distinct from transferring to another planet.  It is generally simpler, and is somewhat similar to an orbital rendezvous, except with the destination having an appreciable amount of gravity.  There are a number of fly-by and insertion maneuvers you can attempt to pull off, especially if you hypothetically add more moons.  I may have some fun with this one and play around with some wacky less-than-sane but efficient options.

Basic Interplanetary Transfers:
In this section I will talk about the idea of transfer windows and some of the more straightforward options for transferring from one body to another.  This is distinct from Planet-Moon transfers in that you are escaping from your home planets gravity well and transferring into that of another.  Its a fundamentally different process in some ways, and is somewhat like the difference between a trip downtown and a multi-state road-trip.  More speed, more complex navigation, much further from home.

Advanced Interplanetary Transfers:
I'll be honest, this probably wont be explained in as great a detail due to the great diversity of options here.  Grabbing fifty gravity assists on a twenty year trip that loops all over the system is going to be different every mission.  The only real common theme is the term 'gravity assist' and being Ebenezer Scrooge with every last millimeter of Delta-V.  I will mention how new kinds of engines are effecting the use of these sorts of trajectories.





sorry for getting this up a little late